Compte tenu de toutes ces irrégularités, et en tablant sur le fait que ces distributions de densités sont vraisemblablement typiques (c'est à dire présentant plus où moins la même physionomie chaque années), il apparaît nécessaire de pratiquer des coefficients de passage en privilégiant les distributions les plus fiables et consistantes (comme je l'envisageais au départ). Autrement, même en optant pour un autre critère que la densité de perfs, on aboutira nécessairement à une grille disproportionnée (et donc contre-productive en pratique).
Dans cette optique, plusieurs configurations sont envisageables suivant les critères que l'on cherche à satisfaire au final.
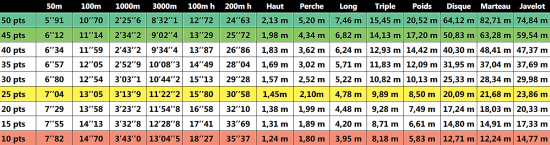
Par exemple, si l'on veut mettre à parité - le plus objectivement possible - sprint et demi-fond, le plus exact serait peut-être d’indexer le 1000 sur la base du 3000 (en dépit de son effectif presque 10 fois moindre), car le niveau y est relativement plus élevé. Pour autant, il me semble préférable d'indexer le 3000 sur la base du 1000, car en plus d'être plus robuste statistiquement, dans l'optique d'un triathlon, cela permettrait aux profils authentiquement endurants de compenser leur désavantage dans les épreuves de puissance en choisissant le 3000 plutôt que le 1000.
Pour les haies, en l'absence de corrections, on a vite fait de se retrouver avec des aberrations, comme par exemple un ratio 100m h/100 m n'évoluant pas comme il devrait, c'est à dire, conformément au fait que moins on est performant sur les haies, moins on est technique, et donc plus grand est l'écart relatif avec le plat. Idem entre le 200m h et le 100 m (plat ou avec haies). Je conçois sans trop de difficultés divers moyens d'y remédier.
Pour le sprint plat, il me parait évident de privilégier le 100 au 50. Les deux ont un à peu près le même effectif, des distributions similaires, mais le niveau de perf est sensiblement meilleur sur 100 m (en dépit du fait que les minimes, faute de technique, sont en général plus performant sur 50). Pour le coef de passage, je dispose pour ce cas particulier d'un outils très précis et efficace. Il s'agit d'une table d'équivalence par tranche de 10 m (du 30 m au 100 m) que j'avais calculé sur la base de centaines de données individuelles produites par des sprinteurs spécialisés, de l'élite mondiale (moins de 10") au sprinteur de niveau départemental (12"). Ces données se laissent très commodément mathématiser et sont donc garantes d'une forte prédictibilité. Ainsi, cette grille permet d'évaluer précisément, quelque soit le niveau, l'équivalence d'une distance à l'autre suivant le profil de sprinteur (du partant mauvais finisseur au finisseur mauvais partant en passant par le profil moyen sur toutes les phases).
Si l'on choisit comme base les valeurs que j'avais donné précédemment (6"12 et 11"14), il est possible d'inférer pour n'importe quel chrono sur 100 m le niveau équivalent sur 50 en tenant compte du profil de base (en l’occurrence un profil typique de minime qui peine à finir un 100 m).
Hélas je ne dispose pas d'un outils similaire pour calculer aussi précisément les équivalences 1000/3000. Dans ce cas là, le plus commode me semble être de procéder à une simple règle de trois comme suggérer précédemment. Franchement, d'expérience, ça fournit une approximation qui n'est pas loin de la réalité (d’avantage que si l'on procédait ainsi pour le 50/100)
Pour les sauts longitudinaux, le triple étant d'un niveau très sensiblement supérieur à la longueur (le 25ème centile y équivaut à peu près au 50ème) et la longueur nettement plus pratiquées, comme pour le 3000, je ne vois pas d'autres moyens simples de garantir l'équivalence que d'opérer une règle de trois en indexant le triple sur la base de son homologue (quoique l'inverse - comme pour le 3000 - puisse être plus objectif en dépit du faible effectif).
Pour le reste, aucun bricolage de ce genre ne m’apparaît nécessaire.